Welcome to the Relation Between Linear And Angular Variables MDCAT MCQs with Answers. In this post, we have shared Relation Between Linear And Angular Variables Multiple Choice Questions and Answers for PMC MDCAT 2024. Each question in MDCAT Physics offers a chance to enhance your knowledge regarding Relation Between Linear And Angular Variables MCQs in this MDCAT Online Test.
Relation Between Linear And Angular Variables MDCAT MCQs Test Preparations
If the radius
𝑟
r is increased, keeping angular velocity
𝜔
ω constant, the linear velocity
𝑣
v will:
a) Increase
b) Decrease
c) Remain the same
d) Become zero
If the angular acceleration
𝛼
α is doubled and the radius
𝑟
r remains constant, the linear acceleration
𝑎
a will:
a) Double
b) Quadruple
c) Remain unchanged
d) Halve
For an object in rotational motion, if the radius
𝑟
r is halved, the linear velocity
𝑣
v will:
a) Halve
b) Double
c) Quadruple
d) Remain unchanged
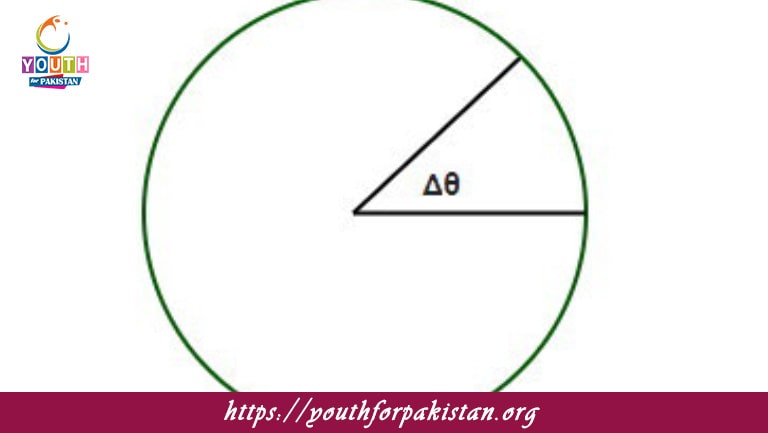
The relationship between angular displacement
𝜃
θ and linear displacement
𝑠
s can be used to find:
a) Angular velocity
b) Linear velocity
c) Angular acceleration
d) Rotational inertia
If the linear velocity
𝑣
v is known and the radius
𝑟
r is increased by a factor of 2, the angular velocity
𝜔
ω will:
a) Halve
b) Double
c) Quadruple
d) Remain unchanged
If the radius of a rotating object is doubled and the angular velocity
𝜔
ω is halved, the linear velocity
𝑣
v will:
a) Remain unchanged
b) Double
c) Quadruple
d) Halve
For a rotating object, if the linear displacement
𝑠
s is constant and the radius
𝑟
r is halved, the angular displacement
𝜃
θ will:
a) Double
b) Halve
c) Quadruple
d) Remain unchanged
If the angular velocity
𝜔
ω is doubled and the radius
𝑟
r remains the same, the linear velocity
𝑣
v will:
a) Double
b) Quadruple
c) Remain unchanged
d) Halve
The formula
𝑎
=
𝑟
⋅
𝛼
a=r⋅α relates which variables in rotational motion?
a) Linear acceleration and angular acceleration
b) Linear velocity and angular velocity
c) Angular displacement and linear displacement
d) Angular acceleration and angular displacement
If the radius
𝑟
r is tripled and the linear velocity
𝑣
v is kept constant, the angular velocity
𝜔
ω will:
a) One-third
b) Double
c) Remain unchanged
d) Triple
𝑣
v is increased while keeping the radius
𝑟
r constant, the angular velocity
𝜔
ω will:
a) Increase proportionally
b) Decrease proportionally
c) Remain the same
d) Become zero
If the angular displacement
𝜃
θ is halved and the radius
𝑟
r remains constant, the linear displacement
𝑠
s will:
a) Halve
b) Double
c) Quadruple
d) Remain unchanged
The relationship between linear and angular variables can be used to find:
a) Rotational inertia
b) Linear momentum
c) Force
d) Work done
If the angular velocity
𝜔
ω is tripled and the radius
𝑟
r remains constant, the linear velocity
𝑣
v will:
a) Triple
b) Double
c) Remain unchanged
d) Quadruple
If the linear velocity
𝑣
v is doubled and the radius
𝑟
r remains constant, the angular velocity
𝜔
ω will:
a) Double
b) Halve
c) Quadruple
d) Remain unchanged
The relation
𝑠
=
𝑟
⋅
𝜃
s=r⋅θ is used to calculate the:
a) Linear displacement
b) Angular velocity
c) Angular acceleration
d) Linear acceleration
If the angular acceleration
𝛼
α is known and the radius
𝑟
r is doubled, the linear acceleration
𝑎
a will:
a) Double
b) Quadruple
c) Remain unchanged
d) Halve
If the radius
𝑟
r is doubled and the linear acceleration
𝑎
a is kept constant, the angular acceleration
𝛼
α will:
a) Halve
b) Double
c) Quadruple
d) Remain unchanged
The relationship between linear and angular variables helps in calculating the:
a) Work done in rotational motion
b) Energy in linear motion
c) Torque
d) Force
If the linear displacement
𝑠
s is known and the radius
𝑟
r is increased, the angular displacement
𝜃
θ will:
a) Decrease
b) Increase
c) Remain unchanged
d) Become zero
The formula
𝑎
=
𝑟
⋅
𝛼
a=r⋅α helps in finding the:
a) Linear acceleration
b) Angular acceleration
c) Angular velocity
d) Linear velocity
For a constant angular velocity
𝜔
ω, if the radius
𝑟
r is doubled, the linear velocity
𝑣
v will:
a) Double
b) Quadruple
c) Remain unchanged
d) Halve
If the angular acceleration
𝛼
α is increased while keeping the radius
𝑟
r constant, the linear acceleration
𝑎
a will:
a) Increase
b) Decrease
c) Remain unchanged
d) Become zero
If you are interested to enhance your knowledge regarding Physics, Chemistry, Computer, and Biology please click on the link of each category, you will be redirected to dedicated website for each category.