Simple Harmonic Motion MDCAT MCQs with Answers
Welcome to the Simple Harmonic Motion MDCAT MCQs with Answers. In this post, we have shared Simple Harmonic Motion Multiple Choice Questions and Answers for PMC MDCAT 2024. Each question in MDCAT Physics offers a chance to enhance your knowledge regarding Simple Harmonic Motion MCQs in this MDCAT Online Test.
Simple Harmonic Motion MDCAT MCQs Test Preparations
What is the defining characteristic of simple harmonic motion?
A) Motion with constant velocity
B) Motion where the restoring force is proportional to the displacement
C) Motion with constant acceleration
D) Motion with no restoring force
The maximum displacement from the equilibrium position in simple harmonic motion is known as:
A) Frequency
B) Amplitude
C) Wavelength
D) Period
In simple harmonic motion, the restoring force is directed:
A) Away from the equilibrium position
B) Towards the equilibrium position
C) Perpendicular to the direction of motion
D) In the direction of motion
The time taken for one complete cycle of simple harmonic motion is called the:
A) Frequency
B) Wavelength
C) Period
D) Amplitude
The frequency of a simple harmonic oscillator is the reciprocal of:
A) The period
B) The amplitude
C) The velocity
D) The restoring force
The total mechanical energy in simple harmonic motion is:
A) Constant
B) Increasing
C) Decreasing
D) Zero
The acceleration of an object in simple harmonic motion is:
A) Constant
B) Zero at maximum displacement
C) Maximum at the equilibrium position
D) Equal to the velocity
The velocity of an object in simple harmonic motion is maximum at:
A) Maximum displacement
B) Equilibrium position
C) Mid-point between maximum displacement
D) Amplitude
The phase of simple harmonic motion at any point in time is given by:
A) The angular frequency multiplied by time
B) The amplitude
C) The velocity divided by the amplitude
D) The displacement divided by the period
The maximum kinetic energy of a simple harmonic oscillator occurs at:
A) Maximum displacement
B) Equilibrium position
C) Halfway between maximum displacement
D) Zero displacement
The maximum potential energy of a simple harmonic oscillator occurs at:
A) Maximum displacement
B) Equilibrium position
C) Halfway between maximum displacement
D) Zero displacement
In simple harmonic motion, the acceleration is always:
A) Zero
B) Positive
C) Directed opposite to the direction of velocity
D) Proportional to the displacement
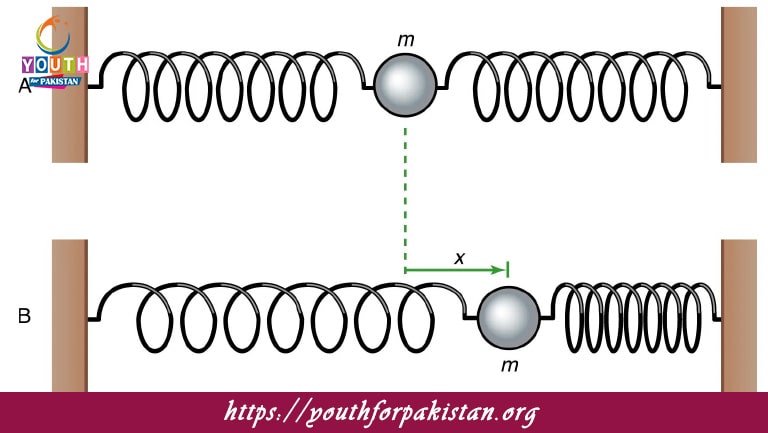
The motion of a mass-spring system can be described as:
A) Simple harmonic motion
B) Uniform circular motion
C) Projectile motion
D) Periodic motion
The frequency of a simple harmonic oscillator depends on:
A) The amplitude of motion
B) The mass of the oscillator and the spring constant
C) The initial velocity
D) The temperature of the environment
The restoring force in a mass-spring system is directly proportional to:
A) The velocity of the mass
B) The displacement of the mass
C) The time
D) The mass of the object
The total energy of a simple harmonic oscillator is:
A) The sum of kinetic and potential energies
B) Equal to the kinetic energy at maximum displacement
C) Equal to the potential energy at equilibrium position
D) Equal to the amplitude squared
In simple harmonic motion, the frequency of oscillation is independent of:
A) Mass of the oscillator
B) Spring constant
C) Amplitude
D) Gravity (for horizontal oscillations)
The phase constant in the equation of simple harmonic motion affects:
A) The amplitude
B) The frequency
C) The initial position of the oscillator
D) The total energy
The displacement of an object in simple harmonic motion is:
A) A function of the square of time
B) A function of time raised to the power of three
C) A sinusoidal function of time
D) A linear function of time
The kinetic energy of an object in simple harmonic motion is maximum when:
A) Displacement is maximum
B) Displacement is zero
C) Velocity is zero
D) Restoring force is maximum
For a simple pendulum with small angular displacements, the motion is:
A) Simple harmonic motion
B) Uniform circular motion
C) Parabolic motion
D) Non-periodic motion
The energy in a simple harmonic oscillator is:
A) Only kinetic
B) Only potential
C) The sum of kinetic and potential energies
D) Zero
In a mass-spring system undergoing simple harmonic motion, the restoring force is:
A) Proportional to the mass
B) Proportional to the velocity
C) Proportional to the square of the displacement
D) Proportional to the displacement
In simple harmonic motion, the displacement is maximum when:
A) The velocity is maximum
B) The acceleration is maximum
C) The potential energy is maximum
D) The kinetic energy is maximum
The phase constant
ϕ affects which aspect of simple harmonic motion?
A) Frequency
B) Amplitude
C) Initial position and direction of motion
D) Total energy
In simple harmonic motion, if the amplitude is doubled, the maximum kinetic energy is:
A) Doubled
B) Tripled
C) Quadrupled
D) Halved
The restoring force in a simple harmonic oscillator is directly related to:
A) The angular frequency and mass
B) The amplitude and velocity
C) The displacement and spring constant
D) The kinetic energy and potential energy
If you are interested to enhance your knowledge regarding Physics, Chemistry, Computer, and Biology please click on the link of each category, you will be redirected to dedicated website for each category.