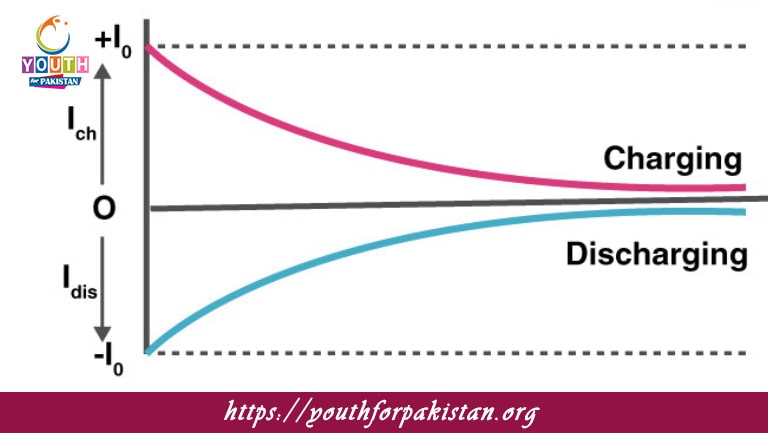
Charging And Discharging A Capacitor MDCAT Quiz is one of the important concepts in electronics and circuit analysis, making it an important topic for MDCAT students. It describes how a capacitor stores electrical energy during charging and releases it when discharging. It is vital to understand the behavior of current, voltage, and time constants during these processes since these principles are applied in both theoretical and practical aspects widely. The exponential equations V=V 0(1−e −t/RC) for charging and V=V 0e −t/RC for discharging form the basis of this topic.
Test Your Skills with an MDCAT Quiz
Try an MDCAT Quiz on charging and discharging capacitors to test your knowledge. These quizzes may contain questions relating to time constants, flow of current, and the role of resistance and capacitance during the process. By practicing such quizzes, students can build a strong grasp of the subject and would be confident enough to solve the problems related to capacitors quickly.
- Test Name: Charging And Discharging A Capacitor MDCAT Quiz
- Type: Quiz Test
- Total Questions: 30
- Total Marks: 30
- Time: 30 minutes
Note: Answer of the questions will change randomly each time you start the test, once you are finished, click the View Results button.
Get Your Username and Password for MDCAT Tests
Sign Up Now
Free Flashcards for Quick Review
Reinforce your learning with Free Flashcards on charging and discharging capacitors. These flashcards make complex ideas, such as the exponential nature of the process and the significance of the RC time constant, very simple. They provide an easy and quick way to revise at the last minute, ensuring that you do not forget the main formulas and concepts when it matters most.
The topic of Charging and Discharging a Capacitor is extremely important for getting good marks in the physics section of the MDCAT. Ace this vital area with our broad resources, quizzes, and flashcards, and be on top in your exam!
The time constant for charging and discharging a capacitor is given by:
τ = RC
The voltage across a charging capacitor increases:
Exponentially
During the charging process, the current in the circuit:
Decreases over time
The time constant τ represents:
The time it takes for the voltage to reach 63% of its maximum value
When a capacitor is discharging, the current:
Decreases exponentially
The voltage across a discharging capacitor decreases:
Exponentially
After a time equal to 5τ, the capacitor is approximately:
Fully discharged
The time constant for charging and discharging a capacitor depends on:
Resistance and capacitance
During the charging process, the capacitor:
Gains charge
The charging of a capacitor in an RC circuit follows:
An exponential curve
During the discharging process, the energy stored in the capacitor:
Decreases
The time for a capacitor to reach 99% of its maximum voltage is approximately:
5τ
The charge on a capacitor at any time t during charging is given by:
Q = C(V)(1 - e^(-t/RC))
In an RC circuit, the current during the charging of a capacitor is:
Maximum at t = 0
The energy stored in a capacitor at full charge is:
E = 1/2 C V²
The capacitor's charge during discharge is:
Q = Q₀ e^(-t/RC)
The discharging time constant is:
τ = RC
The capacitor's voltage at any time t during discharge is given by:
V = V₀ e^(-t/RC)
During discharging, the voltage across the capacitor approaches:
Zero
In a charging capacitor, the voltage across the capacitor at any time t is:
V = V₀ (1 - e^(-t/RC))
The current during the charging process is maximum at:
t = 0
The current in the circuit when the capacitor is fully charged is:
Zero
The voltage across a charging capacitor starts at:
Zero
The time required for a capacitor to discharge to half its initial charge is:
τ
The charging time constant τ is determined by:
The resistance and capacitance in the circuit
In a capacitor discharging circuit, the voltage decreases exponentially until:
It reaches zero
The charging current decreases as the capacitor:
Gains charge
In a capacitor discharge circuit, the initial current is:
Maximum
After one time constant (τ), the charge on a charging capacitor is:
63% of its final value
The capacitor will be fully charged after:
Infinite time
Experience the real exam environment with our expertly designed collection of over 25,000 MCQs MDCAT Mock Tests.
