Stationary Waves MDCAT Quiz with Answers
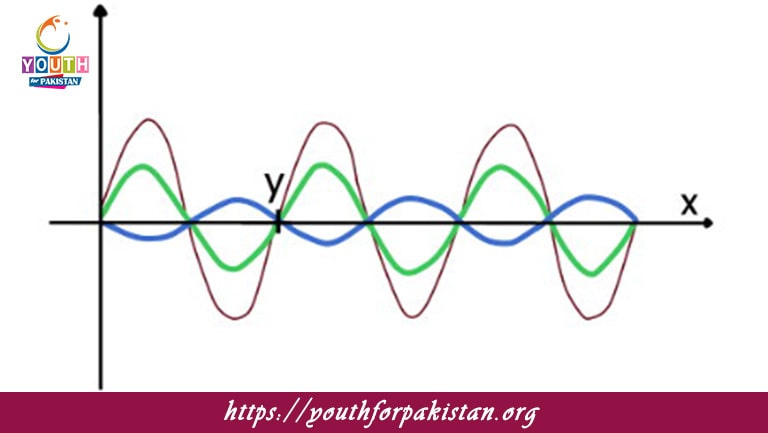
Stationary Waves MDCAT Quiz is otherwise called a standing wave. It’s a wave that remains in a constant position with points of constructive and destructive interference, which don’t travel. Unlike progressive waves, which propagate through a medium, stationary waves appear to be “standing still.” They form when two waves of the same frequency, amplitude, and wavelength travel in opposite directions and interfere with each other. Understanding of stationary waves is very important for MDCAT students, especially in the part dealing with acoustics, vibration, and resonance through different media.
Formation of Stationary Waves
When two waves of identical shape and traveling in opposite directions superpose, they form stationery waves. Such waves may be produced as the result of reflection of a wave at a boundary. A wave traveling along a string or in a tube reflects off a fixed end, and the reflected wave combines with the incident wave to produce a standing wave. Points of constructive interference are called antinodes; those of destructive interference are nodes.
Nodes: These are the points where there is no displacement in the wave since the two interfering waves cancel each other out. At these points, the amplitude of the standing wave is always zero.
Antinodes: These are the points where the displacement is maximum, as the two interfering waves reinforce each other. The amplitude of the wave at these points is maximum.
Characteristics of Stationary Waves
No Energy Transfer: Unlike progressive waves, stationary waves do not transfer energy from one place to another. Instead, the energy oscillates between the nodes and antinodes, which makes stationary waves unique.
Amplitude Variation: The amplitude of a stationary wave varies from zero at the nodes to a maximum at the antinodes. The oscillation is one of the prominent features of stationary waves.
Waveform: The wave pattern seems to be locked in space, and the points of maximum and zero displacement don’t move. This creates a “standing” appearance where the wave doesn’t travel.
Applications of Stationary Waves
Musical Instruments: Many musical instruments are based on the principle of stationary waves. For stringed instruments, for instance, guitars and violins, the stationary waves are the ones produced by the vibrating strings. The stationary waves created by the air column inside a pipe give musical notes in wind instruments such as flutes and organ pipes.
Acoustics: Stationary waves play an important role in the acoustics of rooms and concert halls. The interference patterns of sound waves within a space can lead to regions of constructive interference (loud spots) and destructive interference (quiet spots), which affect the quality of sound.
Resonance: Stationary waves are intimately associated with the phenomenon of resonance, whereby an object oscillates with increasing amplitude when its natural frequency is in accord with that of an applied force. In instruments, this is the principle by which certain frequencies are amplified, resulting in the louder and clearer sounds produced.
MDCAT Quiz: Stationary Waves
MDCAT students may find questions on the formation and properties of stationary waves, including calculation of nodes and antinodes, fundamental frequency, and harmonic overtones. Other types of questions can be solving for wavelength and frequency of stationary waves in strings or air columns and their applications in musical instruments and acoustics.
- Test Name: Stationary Waves MDCAT Quiz
- Type: Quiz Test
- Total Questions: 30
- Total Marks: 30
- Time: 30 minutes
Note: Answer of the questions will change randomly each time you start the test, once you are finished, click the View Results button.
Free Flashcards for Stationary Waves
MDCAT students can strengthen their understanding of wave properties, such as the formation of nodes and antinodes, and the relationship between frequency, wavelength, and harmonic numbers, using free flashcards on stationary waves. It may also include examples from real applications in musical instruments, which would enable students to visualize these concepts in a better way. Regular review of these flashcards will enhance students’ knowledge of stationary waves and, therefore, will be well-prepared for the MDCAT Quiz.

What is the characteristic of a stationary wave?
It results from the superposition of two waves traveling in opposite directions

What is formed when two waves of the same frequency and amplitude travel in opposite directions?
A stationary wave

What does the distance between two adjacent nodes in a stationary wave represent?
Half of the wavelength

How are nodes and antinodes formed in a stationary wave?
By the interference of two waves traveling in opposite directions

What is the relationship between the frequency of the stationary wave and the frequency of the original waves?
They are the same

What is the effect of increasing the frequency on the number of nodes and antinodes in a stationary wave?
The number of nodes and antinodes increases

What is the phase difference between two points at adjacent nodes in a stationary wave?
180° or π radians

How are stationary waves different from progressive waves?
Stationary waves do not transfer energy, while progressive waves do

What is the result of two waves traveling in opposite directions with the same amplitude and frequency?
A stationary wave is formed

What determines the wavelength of a stationary wave?
The distance between two consecutive nodes or antinodes

How does the amplitude of the wave vary in a stationary wave?
It is maximum at the antinodes and zero at the nodes

What is the effect of increasing the amplitude of the waves forming the stationary wave?
The displacement at the antinodes increases

What is the relationship between the frequency and wavelength in a stationary wave?
They are inversely proportional

What happens to the frequency of the stationary wave when the tension in a string is increased?
The frequency increases
Experience the real exam environment with our expertly designed collection of over 25,000 MCQs MDCAT Mock Tests.