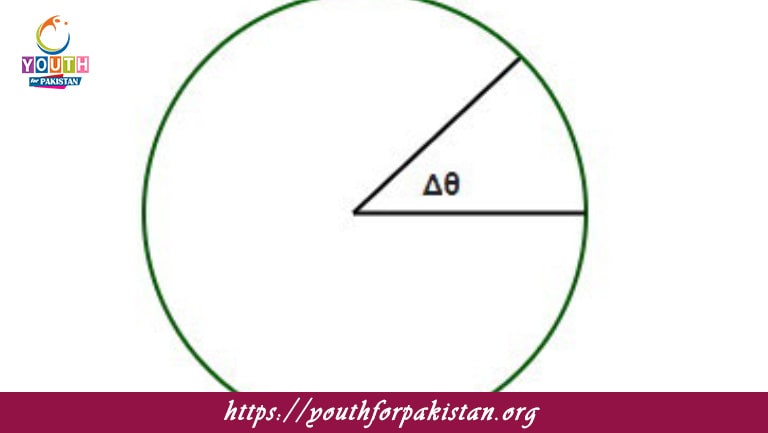
In rotational motion, there exists a fundamental relation between linear and angular variables that enables us to relate the motion of objects in circular paths to their linear counterparts. MDCAT students must understand this relation in order to solve problems relating to rotational dynamics. The basic linear variables involved are displacement, velocity, and acceleration; corresponding to these angular variables are angular displacement, angular velocity, and angular acceleration.
Linear Displacement and Angular Displacement
The relationship between linear displacement (
$\Box$
s) and angular displacement (
????
θ) is given by:
????
=
????
⋅
????
s=r⋅θ
where:
????
s is the linear displacement,
????
r is the radius of the circular path,
????
θ is the angular displacement (in radians).
This equation shows that linear displacement is directly proportional to angular displacement, where the radius is the constant of proportionality. In other words, if an object is rotated through some number of radians, then the linear displacement along the circumference can be found by multiplying the angular displacement by the radius.
Linear Speed and Angular Speed
The relationship between linear velocity (
????
v) and angular velocity (
????
ω) is given by:
????
=
????
⋅
????
v=r⋅ω
where:
????
v is the linear velocity,
????
r is the radius of the circular path,
????
ω is the angular velocity.
This formula demonstrates that the linear velocity of an object moving in a circle is directly proportional to both the radius and the angular velocity. For instance, if the angular velocity increases, then the linear velocity will also increase, provided the radius is kept constant.
Linear Acceleration and Angular Acceleration
Similarly, the relation between linear acceleration (
????
a) and angular acceleration (
????
α) is given by:
????
=
????
⋅
????
a=r⋅α
where:
ℜ
a is the linear acceleration,
????
r is the radius,
????
α is the angular acceleration.
This equation shows that the linear acceleration is directly proportional to the angular acceleration and the radius. The greater the radius of the object’s circular path, the greater the linear acceleration for a given angular acceleration.
MDCAT Quiz: Linear and Angular Variables
In the MDCAT Quiz, students may also be asked to apply these relationships in problems involving rotational and linear motion. For example, they might be asked to find the linear velocity of an object given its angular velocity and the radius of its circular path. Or they might be required to convert angular displacement into linear displacement or angular acceleration into linear acceleration. These problems check the ability of students to switch between linear and angular variables and apply the correct formulas to arrive at the solution.
Free Flashcards for Linear and Angular Variables
Free flashcards, especially those dealing with the relation between linear and angular variables, are a very good study tool for MDCAT students. These flashcards may contain important formulas, practice problems, and examples of how to convert between linear and angular quantities. By regularly going through these flashcards, students can strengthen their understanding of rotational motion and be well-prepared to solve related questions in the MDCAT Quiz. Flashcards are an effective way to master this crucial concept and improve performance in the exam.
Get Your Username and Password for MDCAT Tests
Sign Up Now
