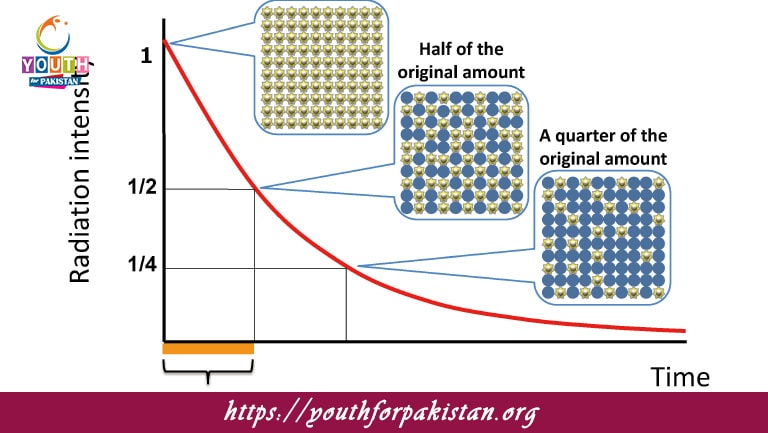
Half Life And Rate Of Decay MDCAT Quiz, the time required by half of the atoms of a sample containing a radioactive substance to decay is called half-life. This concept is an essential part of nuclear physics and describes radioactive decay in a predictable manner. The rate of decay is determined by probabilities that a single atom undergoes decay in a given time frame, which remains constant for a given radioactive isotope. The process of decay in an exponential mode shows a decrease in the quantity of undecayed nuclei by half on every consecutive half-life.
Test Your Knowledge with an MDCAT Quiz
The MDCAT Quiz on Half-Life and Rate of Decay is designed to help you check your skills in computing the amount of the remaining radioactive substance after a certain time or calculating half-life given the decay constant. The quizzes cover such topics as activity calculation, the relationship between half-life and decay constant, and just how the rate of decay affects the stability of radioactive materials. Regular practice will prepare you to solve these problems efficiently in the MDCAT exam.
- Test Name: Half Life And Rate Of Decay MDCAT Quiz
- Type: Quiz Test
- Total Questions: 30
- Total Marks: 30
- Time: 30 minutes
Note: Answer of the questions will change randomly each time you start the test, once you are finished, click the View Results button.
Get Your Username and Password for MDCAT Tests
Sign Up Now
Free Flashcards for Quick Revision
Free Flashcards on Half-Life and Rate of Decay provide quick access to important formulas, including the calculation of half-life, decay constant, and activity of a radioactive sample. These flashcards are an excellent revision tool for rapidly recalling key concepts and formulas that will help you solve questions related to nuclear decay in the MDCAT exam.
The half-life of a radioactive substance is the time required for:
Half of the substance to decay
The rate of decay of a radioactive substance is directly proportional to:
The number of undecayed nuclei
If the half-life of a substance is 5 years, after 10 years, the fraction of the original sample remaining will be:
45661
The relationship between the decay rate and the number of undecayed nuclei is:
Exponential
The half-life of a substance depends on:
The nature of the substance
If a radioactive substance has a half-life of 10 years, then after 20 years, what fraction of the original substance will remain?
45661
The formula for the decay of a radioactive substance is given by:
N = N0 * (1/2)^(t/T)
The rate of decay of a substance can be measured by:
Counting the number of decays per second
The half-life of a substance is independent of:
The quantity of the substance
The rate of decay is inversely proportional to:
The half-life of the substance
If the half-life of a substance is 2 days, how much of it will remain after 6 days?
45665
In the decay of a radioactive substance, the number of remaining atoms decreases:
Exponentially
The half-life of a substance is the time taken for:
Half of the initial amount to decay
The number of particles emitted during radioactive decay is:
Random and unpredictable
The decay rate can be defined as:
The number of decays per unit time
If the half-life of a substance is 4 hours, after 12 hours, what fraction of the original sample remains?
45665
The rate of decay is affected by:
The amount of radioactive substance present
The decay constant is a measure of:
The rate at which a substance decays
The rate of decay can be represented as:
dN/dt = -λN
After 3 half-lives, the remaining fraction of the original sample will be:
45665
The half-life of a substance is defined as:
The time taken for half of the substance to decay
A substance with a short half-life will decay:
Rapidly
The decay of a substance follows:
An exponential decay pattern
After each half-life, the remaining quantity of a substance is reduced by:
Half
The activity of a radioactive substance is measured in:
Becquerels
The half-life of a substance can be calculated if we know:
The decay constant
A longer half-life results in:
A slower decay rate
The time for a radioactive substance to decay by half is called its:
Half-life
If the initial amount of a substance is 100g and the half-life is 10 years, after 20 years, the remaining mass will be:
25g
In radioactive decay, the time interval between each half-life is:
Constant
Experience the real exam environment with our expertly designed collection of over 25,000 MCQs MDCAT Mock Tests.
