Superposition Of Sound Waves MDCAT Quiz with Answers
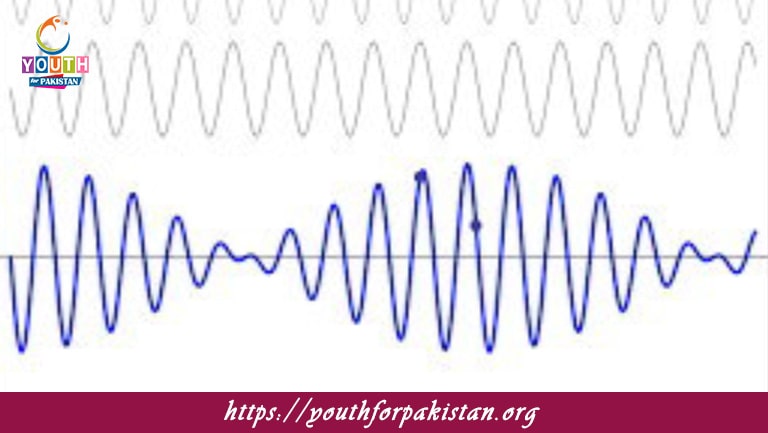
The superposition of sound waves refers to what happens when two or more sound waves meet at a point and combine to form a new wave. This is a basic principle in the theory of waves and applies not only to sound waves but to all kinds of waves, including light and water waves. When sound waves overlap, their displacements add up, resulting in either constructive or destructive interference. The principle of superposition is very important for MDCAT students in the interaction of sound waves and acoustics.
Principles of Superposition
The principle of superposition states that when two or more waves meet, the resultant displacement of the medium is the sum of the displacements of the individual waves at that point in space. This can be expressed mathematically as:
????total=????1+????2+⋯+????????
y total=y 1+y 2+⋯+y n
where:
????totaly total is the displacement of the medium due to the combined effect of all waves,
????1,????2,…,????????y 1,y 2,…,y n are the displacements caused by the individual waves.
In the case of sound waves, each sound wave produces variations in pressure within the air, and these variations add together where the waves overlap.
Types of Interference
When sound waves superimpose, they may either reinforce or cancel out each other. There are two kinds of interference:
Constructive interference occurs when two sound waves are in phase—meaning their displacements are aligned. In the case of constructive interference, the resultant wave has greater amplitude because the displacements add together. Therefore, there is an increase in the intensity or loudness of the sound. For example, when two sources of sound emit the same frequency of sound waves that are perfectly in phase, they will produce a louder sound than either sound would individually.
Destructive Interference: This occurs when two sound waves are out of phase (the crest of one wave coincides with the trough of another wave). In destructive interference, the displacements subtract from each other, leading to a decrease in amplitude. If the waves are perfectly out of phase, they can cancel each other out completely, resulting in silence. This phenomenon is used in noise-canceling headphones, where sound waves generated by the headphones interfere destructively with unwanted ambient noise.
Mathematical Representation of Superposition of Sound Waves
When two sound waves with the same frequency and wavelength overlap, their displacements at any point in space can be represented as:
????
total
=
????
1
sin
(
????
????
−
????
????
)
+
????
2
sin
(
????
????
−
????
????
+
????
)
y
total
=A
1
sin(kx−ωt)+A
2
sin(kx−ωt+ϕ)
where:
????
1
A
1
and
????
2
A
2
are the amplitudes of the individual sound waves,
????
k is the wave number,
????
ω is the angular frequency,
????
t is the time,
????
ϕ is the phase difference between the two waves.
If the waves are in phase (
????
=
0
ϕ=0), they will combine constructively. If the waves are out of phase (
????
=
????
ϕ=π), they will combine destructively.
Applications of Superposition of Sound Waves
Interference Patterns: In environments like concert halls or auditoriums, the superposition of sound waves may result in interference patterns. In some areas, the sound is louder (because of constructive interference), while in others, the sound is softer or even silent (because of destructive interference). This is very important in acoustical design.
Noise-Canceling Technology: Noise-canceling headphones use destructive interference to cancel out unwanted background noise. They work by producing sound waves that are out of phase with the ambient noise, thus canceling it and providing a quieter listening experience.
Beats: When two sound waves of slightly different frequencies interfere, they produce what is known as beats. The periodic variation in loudness is due to constructive and destructive interference. The beat frequency is equal to the difference between the frequencies of the two sound waves. For example, if two tuning forks produce sound waves with frequencies of 440 Hz and 442 Hz, the resulting sound will vary in loudness with a frequency of 2 Hz, producing two beats per second.
Standing Waves: Superposition is also a necessary condition to create standing waves. When the reflected sound wave from any surface interfere with the incident or coming wave at that time, the phenomenon is a standing wave pattern. This happens in musical instruments such as the guitar and organ; the different standing wave patterns are related to different musical notes.
MDCAT Quiz: Superposition of Sound Waves
One can find questions on superposition of sound waves in the MDCAT, particularly questions on constructive and destructive interference, beats, and standing waves. The student may be asked to tell what the resultant intensity of sound would be if two waves interfere or may be asked to solve a problem in which beats are formed. One must understand the mathematical formulation and practical implications of wave superposition to successfully answer these kinds of questions.
Free Flashcards for Superposition of Sound Waves
Free flashcards on the superposition of sound waves help MDCAT students visualize and reinforce key concepts such as interference, beat frequency, and standing waves. The flashcards can have examples of constructive and destructive interference, along with problems to practice calculating beat frequencies and resultant wave patterns. Regular use of these flashcards will deepen students’ understanding of wave behavior and enhance their performance on the MDCAT Quiz.